前置知识:[[费马小定理]],[[二次探测定理]]
实现工具: [[快速幂(模意义下取幂)]], [[快速乘]]
前情提要:
在本文中, 将会使用 p 来代指所要检验是否为质数的数, 用 a 代指选取的底数
1. 梦开始的地方-逆向费马小定理检验
由费马小定理, 有:
对任意素数 p 和与其互质的整数 a ， a^{p-1}\equiv1(mod\ p)
那么是否可以说明, 若对 p, 任意选取一小于 p 且大于 2 的整数 a, 在满足 a^{p-1}\equiv1(mod\ p) 的情况, 可以推出 p 为质数?
很明显不行
,因为存在一些合数满足这个等式.
这些合数被称为费马伪素数，例如最小的费马伪素数为 341=11 \times 31
进一步推导, 既然选择一个数来证明的思路不行, 那么如果选择多个 a, 对多个 a 都满足上述条件, 是否能证明 p 为质数?
很遗憾, 答案依然是不行, 虽然范围被进一步缩小, 但是仍然存在这样一些合数
, 它们被称为卡迈克尔数, 例如 561, 这些数即使遍历 [2, p-1] 范围内的全部整数也能被验证满足条件, 也就是说, 对于这些数, 无法通过多次运用逆向费马小定理证明质数
因此, 我们需要引入第二个检验定理: [[二次探测定理]]
2. 二次探测定理:
对于质数 p ，若 x^2\equiv1(mod\ p) ，则小于 p 的解只有两个, x\equiv1(mod\ p) , x\equiv p-1(mod\ p).
在很多资料中会错误的标记为 x=1,x=p-1 
, 这实际上是错误的, 并且容易导致误解
如果将二次探测定理与逆向费马小定理检验结合, 我们就得到了Miller Rabin 素数判定的完全体, 在Miller Rabin 素数判定方法中, 对于选取的某一个 a, 我们不再像逆向费马小定理检验中提到的那样, 仅对 a^{p-1}\equiv1(mod\ p) 的正确性进行检验, 而是根据二次探测定理, 在已选定的 a 的基础上, 进行一系列的检验, 这样就能够大大提高检验的正确率
3. Miller Rabin 素数判定
我们继续 :
对于二次检测定理, 我们已经知道对于质数 p ，若 x^2\equiv1(mod\ p) ，则小于 p 的解只有两个, x\equiv1(mod\ p) , x\equiv p-1(mod\ p).
换而言之, 若是 x\mod\ p 的结果不为 1 或者 p-1, 就可以得出 p 不是质数
进一步考虑:
如果对于 p 检测得到 a^{p-1}\equiv1(mod\ p) ，且 p-1 为偶数（ p 为偶数会直接特判筛掉, 所以 p-1 必为偶数）
变换之后可得到:
(a^{\frac{p-1}{2}})^2\equiv1(mod\ p)
那么我们就可以对 a^{\frac{p-1}{2}} \mod p 的结果进行检验, 如果为 1 或者 p-1, 就继续检验, 直到出现不符合的结果为止.
这个过程可以进行多少次呢? 这取决于 p-1 能够被分解的次数, 也就是 p-1=u 2^r ,r 为几即可分解几次, 例如对于 p=13 的情况, 就可以分别对 a^3, a^6, a^{12} 的情况进行检验
但是, 在实际检验中, 我们的顺序需要调转, 也就是从低次幂向高次幂进行检验, 这是为什么呢? 我们需要对多次进行二次检验的过程分析:
当我们已经通过检验得知 x\equiv1(mod\ p) ,或是 x\equiv p-1(mod\ p). 就可以推出 x^2\equiv1(mod\ p), 进一步就可以推出 x^4\equiv1(mod\ p), 所以只要 x \mod p 等于 1 或者 p-1, 之后的 x^2, x^4 ,它们 \mod p 的结果一定都是 1
我们从 a^u 开始进行判定, 如果 a^u \mod p 的结果不是 1 或者 p-1, 这没有关系, 因为可能 a^{u2^1}\equiv p-1(mod\ p) ,如果 a^{u 2^1} \mod p 的结果也不是 1 或者 p-1, 我们还可以继续下去, 直到出现 \mod p 的结果为 1 或者 p-1 的情况为止, 因为如果
- 结果为 1, 那就说明对于一个 x^2\equiv1(mod\ p) 的情况下, 我们知道 x\mod\ p 不为 1 或者 p-1, 那么就可以推导出 p 不是质数
- 结果为 p-1, 那么接下来的 \mod p 的结果一定全部为 1, 也就是对于选定的这个 a, 无法证明 p 是合数, 应该换一个 a 进行检测
并且补充一点:
当 a^{u 2^r} 的情况下要特殊判断, \mod p 的结果不能为 p-1, 否则就连费马小定理也不满足了
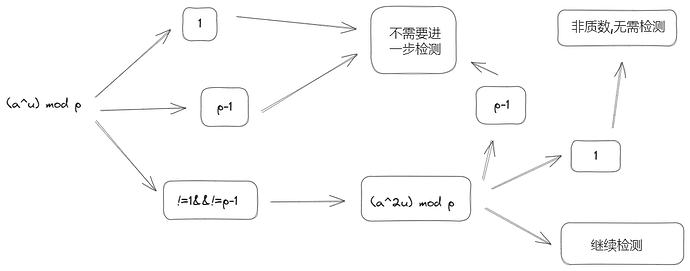
流程图:
总结:
经过以上的分析, 我们可以将检测过程概括为以下两条规则, 如果满足这两条规则中的任一一条, 我们就可以说对于选定的这个 a, 无法证明 p 是合数
- a^u \equiv 1(mod\ p), 因为当 a^u \equiv 1 (mod\ p), 我们自然可以推出接下来的 a^u,a^{u\times2},a^{u\times2^2}… 在 \mod p 之后的结果全部都为 1, 所以无需进一步验证
- a^{u2^d} \equiv 1 (mod\ p) ,其中 d 满足 0 \leq d \leq r - 1 , r 为 p-1 被分解的次数 (p-1=u 2^r)
接下来就可以编写代码了:
代码
long long qmul(long long a,long long b,long long mod)//快速乘
{
long long c=(long double)a/mod*b;
long long res=(unsigned long long)a*b-(unsigned long long)c*mod;
return (res+mod)%mod;
}
long long qpow(long long a,long long n,long long mod)//快速幂
{
long long res=1;
while(n)
{
if(n&1) res=qmul(res,a,mod);
a=qmul(a,a,mod);
n>>=1;
}
return res;
}/
bool MillerRabin(long long n)
{
if(n<3||n%2==0) return n==2;//特判小于3和偶数情况
long long u=n-1,t=0;
while(u%2==0) u/=2,++t;
long long ud[]={2,325,9375,28178,450775,9780504,1795265022};
for(long long a:ud)
{
long long v=qpow(a,u,n);
if(v==1||v==n-1||v==0) continue;//从一开头就满足了条件,这个a就无法排除n为合数可能性
for(int j=1;j<=t;j++)
{
v=qmul(v,v,n);
if(v==n-1&&j!=t){
v=1;
break;
}//出现一个n-1，后面都是1，直接跳出
if(v==1) return 0;//这里代表前面的解不为1或者n-1,即n不是质数,二次检验失败
}
if(v!=1) return 0;//Fermat检验
}
return 1;
}
选取底数的方法
在 wiki 上我们可以查找到:
- 对于小于 2^{32} 的情况, 选取 2,7,61 三个底数即可将判断错误的概率降至 0
- 对于小于 2^64 的情况, 选取 2,325,9375,28178,450775,9780504,1795265022 同理
这样就不用担心运气不好啦