前面的文章,我们介绍了深度优先搜索,所以由可知 DFS 是以深度作为第一关键词的,即当碰到岔道口时总是先选择其中的一条岔路前进,而不管其他岔路,直到碰到死胡同时才返回岔道口并选择其他岔路。
接下来我们将介绍的广度优先搜索(Breadth First Search,BFS)则是以广度为第一关键词,当碰到岔道口时,总是先依次访问从该岔道口能直接到达的所有结点,然后再按这些结点被访问的顺序去依次访问它们能直接到达的所有结点,以此类推,直到所有结点都被访问为止。
这就跟平静的水面中投入一颗小石子一样,水花总是以石子落水处为中心,并以同心圆的方式向外扩散至整个水面,见下图这个,从这点来看和 DFS 那种沿着一条线前进的思路是完全不同的。


为了讨论广度优先搜索是如何实现的,以深度优先搜索的迷宫为例,具体见下图。
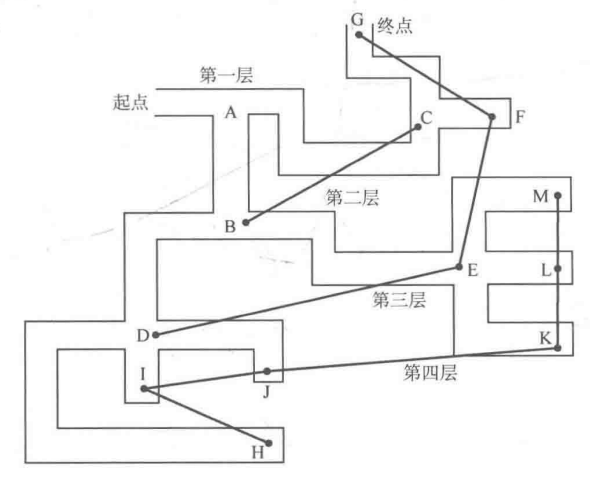

同时也要注意,需要在广度优先搜索的过程中得出从起点到出口的最少步数(相邻两个能够直接到达的字母为一步):
① 访问 A (第一层),发现从 A 出发能到达 B 和 C (第二层),因此接下来需要访问 B 和 C 。
② 访问 B (第二层),发现从 B 出发能到达 D 和 E (第三层),因此待第二层的结点全部访问完毕后需要访问 D 和 E。
③ 访问 C (第二层),发现从 C 出发能到达 F 和 G (第三层),因此待第二层的结点全部访问完毕后需要访问 F 和 G ,且它们排在 D 和 E 之后。
④ 由于第二层访问完毕,因此需要访问第三层。访问 D (第三层),发现从 D 出发能到达 H、I、J (第四层),因此待第三层的结点全部访问完毕后需要访问 H、I、J 。
⑤ 访问 E(第三层),发现从 E 出发能到达 K、L、M(第四层),因此待第三层的结点全部访问完毕后需要访问 K、L、M 。
⑥ 访问 F (第三层),发现 F 是死胡同,没有能直接到达的新结点,因此不予理睬。
⑦ 访问 G (第三层),发现 G 是出口,算法结束,至于那些第四层还没有访问的结点,就可以不用去访问了。
如上图所示,A 为第一层,BC 为第二层,DEFG 为第三层,HIJKLM 为第四层,并且这个层数就是从初始点 A 出发到达相应结点所需要的步数。
由此可以知道,从起点 A 到出口 G 的最少步数为 3 (因为G在第三层)。
由上面的例子还可以发现,整个算法的过程很像一个队列,并且模拟的过程是这样的(可以与前面的步骤对照起来看):
① 先在队列中放置初始点 A,然后取出队首元素 A,将 A直接相连的 B 与 C 入队,此时队列内元素为 {B,C} 。
② 队首元素 B 出队,将 B 直接相连的 D 与 E 入队,此时队列内元素为 {C,D,E}。
③ 队首元素 C 出队(注意:队列的特性是先进先出,因此这里不是 D 出队),将 C 直接相连的 F 与 G 入队,此时队列内元素为 {D,E,F,G} 。
④ 队首元素 D 出队,将 D 直接相连的 H、I、J 入队,此时队列内元素为 {E,F,G,H,I,J} 。
⑤ 队首元素E出队,将 E 直接相连的 K、L、M 入队,此时队列内元素为 {F,G,H,I,J,K,L,M} 。
⑥ 队首元素F出队,没有与 F 直接相连的新结点,此时队列内元素为 {G,H,I,J,K,L,M} 。
⑦ 队首元素 G 出队,找到出口,算法结束。
因此广度优先搜索(BFS)一般由队列实现,且总是按层次的顺序进行遍历,其基本写法如下(可作模板用):
void BFS(int s)
{
queue<int> q;
q.push(s);
while(!q.empty())
{
取出队首元素 top;
访问队首元素 top;
将队首元素出队;
将 top的下一层结点中未曾入队的结点全部入队,并设置为已入队;
}
}
下面是对该模板中每一个步骤的说明,请结合代码一起看:
① 定义队列 g,并将起点 s 入队。
② 写一个 while 循环,循环条件是队列 q 非空。
③ 在 while 循环中,先取出队首元素 top,然后访问它(访问可以是任何事情,例如将其输出)。访问完后将其出队。
④ 将 top 的下一层结点中所有未曾入队的结点入队,并标记它们的层号为 now 的层号加 1,同时设置这些入队的结点已入过队。
⑤ 返回 ② 继续循环。
下面举一个例子,希望大家能从中学习 BFS 的思想是如何通过队列来实现的,并能尝试学习写出本例的代码。
给出一个 m×n 的矩阵,矩阵中的元素为 0 或 1。
位置 (x,y) 与其上下左右四个位置 (x,y+1)、(x,y-1)、(x+1,y)、(x-1,y)是相邻的。
如果矩阵中有若干个 1 是相邻的(不必两两相邻),那么称这些 1 构成了一个 “块” 。
求给定的矩阵中 “块” 的个数。
0 1 1 1 0 0 1
0 0 1 0 0 0 0
0 0 0 0 1 0 0
0 0 0 1 1 1 0
1 1 1 0 1 0 0
1 1 1 1 0 0 0
例如上面的 6×7 的矩阵中, “块” 的个数为 4。
对这个问题,求解的基本思想是:枚举每一个位置的元素,如果为 0 ,则跳过;如果为 1 ,则使用 BFS 查询与该位置相邻的 4 个位置(前提是不出界),判断它们是否为 1 (如果某个相邻的位置为 1 ,则同样去查询与该位置相邻的 4 个位置,直到整个 “1” 块访问完毕)。
而为了防止走回头路,一般可以设置一个 bool 型数组 ing(即 in queue 的简写)来记录每个位置是否在 BFS 中已入过队。
一个小技巧是:对当前位置 (x,y) 来说,由于与其相邻的四个位置分别为 (x,y+1)、(x,y-1)、(x+1,y)、(x-1,y),那么不妨设置下面两个增量数组,来表示四个方向(竖着看即为(0,1)、(0,-1)、(1,0)、(-1,0)。
int x[] = {0,0,1,-1};
int Y[] = {1,-1,0,0};
这样就可以使用 for 循环来枚举 4 个方向,以确定与当前坐标 (nowX,nowY) 相邻的 4 个位置,如下所示:
for(int i=0;i<4;i++)
{
newX = nowX + X[i];
newY = nowY + Y[i];
}
下面给出本例的代码,希望能仔细理解代码中 BFS 的写法,并在之后尝试自己独立重写:
#include <cstdio> #include <queue> using namespace std;
const int maxn = 100;
struct node {
int x,y; //位置(x,y) }Node;
int n,m; // 矩阵大小为 n*m int matrix[maxn][maxn]; // 01 矩阵 bool inq[maxn][maxn]={false}; // 记录位置 (x,y) 是否已入过队
int X[4] = {0,0,1,-1}; //增量数组 int Y[4] = {1,-1,0,0};
bool judge (int x,int y) //判断坐标 (x,y) 是否需要访问 {
//越界返回false if(x>=n||x<0||y>=m||y<0) return false;
//当前位置为 0,或 (x,y) 已入过队,返回 false if(matrix[x][y]==0||inq[x][y]==true) return false;
//以上都不满足,返回 true return true;
}
// BFS 函数访问位置 (x,y) 所在的块,将该块中所有 "1" 的 inq 都设置为 true void BFS(int x,int y)
{
queue<node>Q; //定义队列 Node.x = x,Node.y = y; //当前结点的坐标为(x,y) Q.push (Node); //将结点 Node 入队 inq[x][y] = true; //设置 (x,y) 已入过队 while(!Q.empty())
{
node top=Q.front(); //取出队首元素 Q.pop(); //队首元素出队 for(int i=0;i<4;i++)
{
//循环4次,得到4个相邻位置 int newX = top.x + X[i];
int newY = top.y + Y[i];
if(judge(newX,newY))
{
//设置 Node 的坐标为 (newX,newY) Node.x=newX,Node.y=newY;
Q.push(Node); //将结点 Node 加入队列 inq[newX][newY]=true;//设置位置 (newx,newY) 已入过队 }
}
}
}
int main()
{
scanf("%d%d",&n,&m);
for(int x=0;x<n;x++)
{
for(int y=0;y<m;y++)
{
scanf("%d",&matrix[x][y]); //读入01矩阵 }
}
int ans=0; //存放块数 for(int x=0;x<n;x++) //枚举每一个位置 {
for(int y=0;y<m;y++)
{
//如果元素为1,且未入过队 if(matrix[x][y]==1&&inq[x][y]==false)
{
ans++; //块数加 1 BFS(x,y); //访问整个块,将该块所有 "1" 的 inq 都标记为 true }
}
}
printf("%d\n",ans);
return 0;
}
接下来再看一个类似的例子。
给定一个 n * m 大小的迷宫,其中 * 代表不可通过的墙壁,而 “.” 代表平地,S 表示起点,T 代表终点。
移动过程中,如果当前位置是 (x,y) (下标从 0 开始),且每次只能前往上下
左右 (x,y+1)、(x,y-1)、(x-1,y)、(x+1,y) 四个位置的平地,求从起点 S 到达终点 T 的最少步数。
.....
.*.*.
.*S*.
.***.
...T*
在上面的样例中,S 的坐标为 (2,2),T 的坐标为(4,3) 。
在本题中,由于求的是最少步数,而 BFS 是通过层次的顺序来遍历的,因此可以从起点 S 开始计数遍历的层数,那么在到达终点 T 时的层数就是需要求解的起点 S 到达终点 T 的最少步数。
于是可以写出下面的代码:
#include <cstdio> #include <cstring> #include <queue> using namespace std;
const int maxn = 100;
struct node
{
int x,y; // 位置(x,y) int step; // step 为从起点 S 到达该位置的最少步数(即层数) }S,T,Node; // S 为起点,T 为终点,Node 为临时结点 int n,m; // n为行,m为列 char maze [maxn] [maxn]; // 迷宫信息
bool inq[maxn][maxn] = {false};//记录位置(x,y)是否已入过队
int X[4]={0,0,1,-1}; //增量数组 int Y[4] = {1,-1,0,0};
//检测位置(x,y)是否有效
bool test(int x,int y)
{
if(x>=n||x<0||y>=m||y<0) return false; //超过边界 if(maze[x][y] == '*') return false; //墙壁* if(inq[x][y] == true) return false; //已入过队 return true; //有效位置 }
int BFS()
{
//定义队列 queue<node> q;
q.push(S); //将起点 s入队 while(!q.empty())
{
node top = q.front(); //取出队首元素 q.pop(); //队首元素出队 if(top.x == T.x && top.y == T.y)
{
return top.step; //终点,直接返回最少步数 }
for(int i=0;i<4;i++)
{ //循环 4 次,得到 4 个相邻位置 int newX=top.x+X[i];
int newY=top.y+Y[i]; //位置 (newX,newY)有效 if(test(newX,newY))
{
//设置Node 的坐标为(newX,newY) Node.x=newX,Node.y=newY;
Node.step=top.step+1; // Node 层数为 top 的层数加1 q.push(Node); // 将结点 Node 加入队列 inq[newX][newY]=true; //设置位置 (newX,newY) 已入过队 }
}
}
return -1; //无法到达终点T时返回-1 }
int main()
{
scanf("%d%d",&n,&m);
for(int i=0;i<n;i++)
{
getchar(); //过滤掉每行后面的换行符 for(int j=0;j<m;j++)
{
maze[i][j]=getchar();
}
maze[i][m+1]='\0';
}
scanf("%d%d%d%d",&S.x,&S.y,&T.x,&T.y); //起点和终点的坐标 S.step=0;//初始化起点的层数为 0,即 s 到s 的最少步数为0 printf("%d\n",BFS());
return 0;
}
输入数据:
5 5 //5行5列 ..... //迷宫信息 .*.*.
.*S*.
.***.
...T*
2 2 4 3 //起点S的坐标与终点T的坐标
输出数据:
11
上面的代码希望大家能耐心地把它读懂,然后自己动手写一写,这对后面两个章节中树与图的遍历的学习大有帮助。
再强调一点,在 BFS 中设置的 ing 数组的含义是判断结点是否已入过队,而不是结点是否已被访问。
区别在于:如果设置成是否已被访问,有可能在某个结点正在队列中(但还未访问)时由干其他结点可以到达它而将这个结点再次入队,导致很多结点反复入队,计算量大大增加。因此 BFS 中让每个结点只入队一次,故需要设置 ing 数组的含义为结点是否已入过队而非结点是否已被访问。
最后指出,当使用 STL的 queue 时,元素入队的 push操作只是制造了该元素的一个副本入队,因此在入队后对原元素的修改不会影响队列中的副本,而对队列中副本的修改也不会改变原元素,需要注意由此可能引入的 bug(一般由结构体产生)。例如下面这个例子:
#include <cstdio> #include <queue> using namespace std;
struct node {
int data;
}a[10];
int main ()
{
queue<node> q;
for(int i=1;i<=3;i++)
{
a[i].data=i; //a[1]=1,a[2]=2,a[3]=3 q.push (a[i]);
}
//尝试直接把队首元素(即 a[1])的数据域改为 100 q.front().data=100;
//事实上对队列元素的修改无法改变原元素 printf("%d %d %d\n",a[1].data,a[2].data,a[3].data);
//然后尝试直接修改 a[1] 的数据域为200(即 a[1],上面已经修改为100) a[1].data=200;
//事实上对原元素的修改也无法改变队列中的元素 printf("%d\n",q.front().data);
return 0;
}
输出结果:
1 2 3
100
这就是说,当需要对队列中的元素进行修改而不仅仅是访问时,队列中存放的元素最好
不要是元素本身,而是它们的编号(如果是数组的话则是下标)。
例如,把上面的程序改成这样:
#include <cstdio> #include <queue> using namespace std;
struct node
{
int data;
}a[10];
int main()
{
queue<int> q; //q存放结构体数组中元素的下标 for(int i=1;i<=3;i++)
{
a[i].data = i; //a[1]=1,a[2]=2,a[3]=3 q.push(i); //这里是将数组下标i入队,而不是结点a[i]本身 }
a[q.front()].data=100; //q.front() 为下标,通过a[q.front()]即可修改原元素 printf("%d\n",a[1].data);
return 0;
}
输出结果:
100
这个小技巧可以避免很多由使用 queue 不当导致的错误,因此我们需要仔细体会这种写法和前面那种写法的区别,就可以在写 BFS 时避免一些错误的发生。

