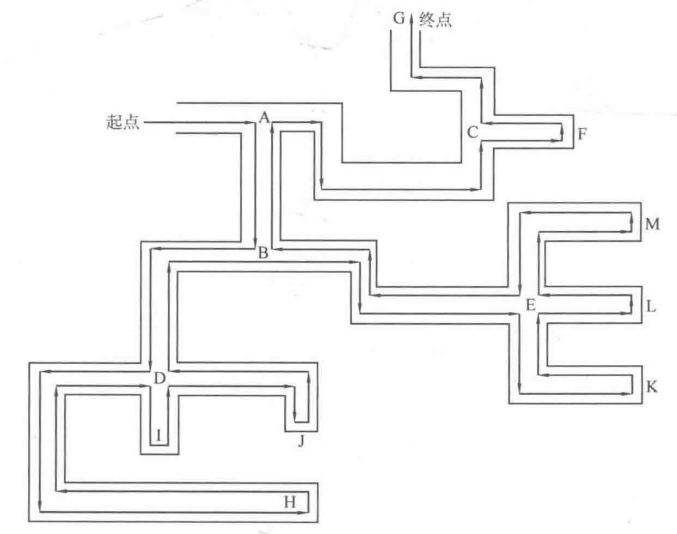
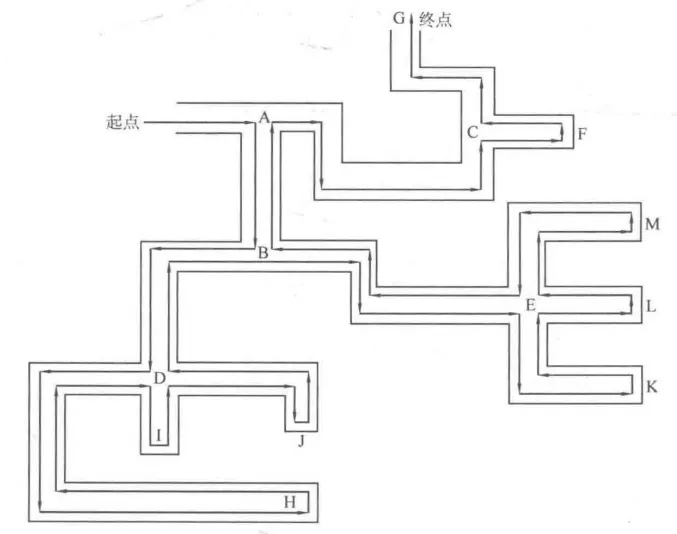
设想我们现在以第一视角身处一个巨大的迷宫当中,没有上帝视角,没有通信设施,更没有热血动漫里的奇迹,有的只是四周长得一样的墙壁。于是,我们只能自己想办法走出去。
如果迷失了内心,随便乱走,那么很可能被四周完全相同的景色绕晕在其中,这时只能放弃所谓的侥幸,而去采取下面这种看上去很盲目但实际上会很有效的方法。
以当前所在位置为起点,沿着一条路向前走,当碰到岔道口时,选择其中一个岔路前进。
如果选择的这个岔路前方是一条死路,就退回到这个岔道口,选择另一个岔路前进。如果岔路中存在新的岔道口,那么仍然按上面的方法枚举新岔道口的每一条岔路。这样,只要迷宫存在出口,那么这个方法一定能够找到它。
可能有读者会问,如果在第一个岔道口处选择了一条没有出路的分支,而这个分支比较深,并且路上多次出现新的岔道口,那么当发现这个分支是个死分支之后,如何退回到最初的这个岔道口?
其实方法很简单,只要让右手始终贴着右边的墙壁一路往前走,那么自动会执行上面这个走法,并且最终一定能找到出口。下图即为使用这个方法走一个简单迷宫的示例。
从上图可知,从起点开始前进,当碰到岔道口时,总是选择其中一条岔路前进(例如图中总是先选择最右手边的岔路),在岔路上如果又遇到新的岔道口,仍然选择新岔道口的其中一条岔路前进,直到碰到死胡同才回退到最近的岔道口选择另一条岔路。
也就是说,当碰到岔道口时,总是以"深度"作为前进的关键词,不碰到死胡同就不回头,因此把这种搜索的方式称为深度优先搜索(Depth First Search,DFS)。
从迷宫的例子还应该注意到,深度优先搜索会走遍所有路径,并且每次走到死胡同就代表一条完整路径的形成。这就是说,深度优先搜索是一种枚举所有完整路径以遍历所有情况的搜索方法。
那么如何来实现深度优先搜索(DFS)呢?
在上图中,把迷宫中的关键结点(岔道口或死胡同)用字母代替,然后来看看在DFS的过程中是如何体现在这些关键结点上的(已经在图中标记了字母):
① 从第一条路可以得到先后访问的结点为 ABDH,此时 H 到达了死胡同,于是退回到D;再到 I ,但是 I 也是死胡同,再次退回到 D;接着来到 J ,很不幸 J 还是死胡同,于是退回到 D ,但是此时 D 的岔路已经走完了,因此退回到上一个岔道口 B。
② 从 B 到达 E ,接下来又是三条岔路(K、L、M),依次进行枚举;前往 K ,发现 K 是死胡同,退回到 E;前往 L ,发现 L 是死胡同,退回到 E ;前往 M,发现 M 是死胡同,退回到 E 。
最后因为 E 的岔路都访问完毕了,于是退回到 B 。但是 B 的所有岔路( D 和 E)也都访问完了,因此退回到 A。
③ 访问 A 的另一个岔路可以到达 C ,而 C 仍然有两条岔路( F 和 G ),于是先访问 F ,发现 F 是死胡同,退回到 C ;再访问 G ,发现是出口,DFS 过程结束,整个 DFS 过程中先后访问结点的顺序为 ABDHIJEKLMCFG 。
这个过程是不是和出栈入栈的过程很相似?
第一步,ABD 入栈,然后把 D 的三条岔路 HIJ 先后入栈和出栈,再把 D 出栈;第二步和第三步执行与第一步类似的操作,我们不妨自己模拟出栈与入栈的过程。
由此可以知道如何去实现深度优先搜索;先对问题进行分析,得到岔道口和死胡同;
再定义一个栈,以深度为关键词访问这些岔道口和死胡同,并将它们入栈;而当离开这些岔道口和死胡同时,将它们出栈。
因此,深度优先搜索(DFS)可以使用栈来实现。
这听起来很容易,但是实现起来却并不轻松,有没有既容易理解又容易实现的方法呢?
有的——递归。
现在从 DFS 的角度来看求解 Fibonacci 数列的过程。
回顾一下 Fibonacci 数列的定义:F(0)=1,F(1)=1,F(n)=F(n-1)+F(n-2)(n≥2)。
可以从这个定义中挖掘到,每当将 F(n) 分为两部分 F(n-1) 与 F(n-2) 时,就可以把 F(n) 看作迷宫的岔道口,由它可以到达两个新的关键结点 F(n-1) 与 F(n-2) 。
而之后计算 F(n-1) 时,又可以把 F(n-1) 当作在岔道口 F(n) 之下的岔道口。
既然有岔道口,那么一定有死胡同。很容易想象,当访问到 F(0) 和 F(1) 时,就无法再向下递归下去,因此 F(0) 和 F(1) 就是死胡同。
这样说来,递归中的递归式就是岔道口,而递归边界就是死胡同,这样就可以把如何用递归实现深度优先搜索的过程理解得很清楚。
为了使上面的过程更清晰,可以直接来分析递归图,如下图:
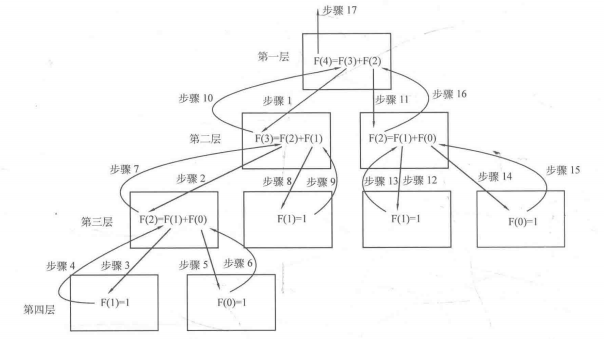
可以在递归图中看到,只要 n>1,F(n) 就有两个分支,即把 F(n) 当作岔道口;而当 n为 1 或 0 时,F(1) 与 F(1) 就是迷宫的死胡同,在此处程序就需要返回结果。这样当遍历完所有路径(从顶端的 F(4)到底层的所有F(1)与 F(0))后,就可以得到 F(4)的值。
因此,使用递归可以很好地实现深度优先搜索。
这个说法并不是说深度优先搜索就是递归,只能说递归是深度优先搜索的一种实现方式,因为使用非递归也是可以实现 DFS 的思想的,但是一般情况下会比递归麻烦。
不过,使用递归时,系统会调用一个叫系统栈的东西来存放递归中每一层的状态,因此使用递归来实现 DFS 的本质其实还是栈。
接下来讲解一个例子,读者需要从中理解其中包含的 DFS 思想,并尝试学习写出本例的代码。
有 n 件物品,每件物品的重量为 w[i] ,价值为 c[i] 。
现在需要选出若干件物品放入一个容量为 V 的背包中,使得在选入背包的物品重量和不超过容量 V 的前提下,让背包中物品的价值之和最大,求最大价值。(1≤n≤20)
在这个问题中,需要从 n 件物品中选择若干件物品放入背包,使它们的价值之和最大。
这样的话,对每件物品都有选或者不选两种选择,而这就是所谓的"岔道口"。
那么什么是 “死胡同” 呢?——题目要求选择的物品重量总和不能超过 V,因此一旦选择的物品重量总和超过 V ,就会到达 “死胡同”,需要返回最近的 “岔道口” 。
显然,每次都要对物品进行选择,因此 DFS 函数的参数中必须记录当前处理的物品编号 index。
而题目中涉及了物品的重量与价值,因此也需要参数来记录在处理当前物品之前,已选物品的总重量 sumW 与总价值 sumC 。
于是 DFS函数看起来是这个样子:
void DFS(int index,int sumW,int sumC){...}
于是,如果选择不放入 index 号物品,那么 sumW 与 sumC 就将不变,接下来处理 index +1号物品,即前往 DFS(index+1,sumW,sumC) 这条分支;而如果选择放入 index 号物品,那么 sumW 将增加当前物品的重量 w[index],sumC 将增加当前物品的价值c[index],接着处理 index+1号物品,即前往 DFS(index+1,sumW+w[index], sumC+c[index])这条分支。
一旦 index 增长到了 n,则说明已经把 n 件物品处理完毕(因为物品下标为从 0 到 n-1 ),此时记录的 sumW 和 sumC 就是所选物品的总重量和总价值。
如果 sumW 不超过 V 且 sumC 大于一个全局的记录最大总价值的变量 maxValue,就说明当前的这种选择方案可以得到更大的价值,于是用 sumC 更新 maxValue。
下面的代码体现了上面的思路,请注意 “岔道口” 和 “死胡同” 在代码中是如何体现的:
#include <cstdio> const int maxn=30;
int n,V,maxValue = 0; //物品件数 n,背包容量 V,最大价值 maxValue int w[maxn],c[maxn]; //w[i] 为每件物品的重量,c[i] 为每件物品的价值 //DFS,index为当前处理的物品编号 //sumW 和 sumC 分别为当前总重量和当前总价值 void DFS(int index,int sumW,int sumC)
{
if(index==n)
{
//已经完成对 n 件物品的选择(死胡同) if(sumW<=V&&sumC>maxValue)
{
maxValue=sumC; //不超过背包容量时更新最大价值maxValue }
return;
}
//岔道口 DFS(index+1,sumW,sumC); //不选第 index 件物品 DFS(index+1,sumW+w[index],sumC+c[index]); //选第index件物品 int main()
{
scanf ("%d%d",&n,&V);
for(int i=0;i<n;i++)
{
scanf("%d",&w[i]); //每件物品的重量 }
for(int i=0;i<n;i++)
{
scanf("%d",&c[i]); //每件物品的价值 }
DFS(0,0,0); //初始时为第0件物品、当前总重量和总价值均为0 printf("%d\n",maxValue);
return 0;
}
输入数据:
5 8 // 5 件物品,背包容量为 8
3 5 1 2 2 //重量分别为 3 5 1 2 2
4 5 2 1 3 //价值分别为 4 5 2 1 3
输出结果:
10
可以注意到,由于每件物品有两种选择,因此上面代码的复杂度为O(2n),这看起来不是很优秀。
但是可以通过对算法的优化,来使其在随机数据的表现上有更好的效率。
在上述代码中,总是把 n 件物品的选择全部确定之后才去更新最大价值,但是事实上忽视了背包容量不超过 V 这个特点。
也就是说,完全可以把对 sumW 的判断加入 “岔道口” 中,只有当 sumW≤V 时才进入岔道,这样效率会高很多,代码如下:
void DFS(int index,int sumW,int sumC)
{
if(index==n)
{
return; //已经完成对n件物品的选择
}
DFS(index+1,smW,sumC); //不选第 index件物品
//只有加入第 index 件物品后未超过容量 V,才能继续
if(sumW+w[index]<=V)
{
if(sumC+c[index]>ans)
{
ans=sumC+c[index]; //更新最大价值maxValue
}
DFS(index+1,sumW+w[index],sumC+c[index]);//选第index件物品
}
}
可以看到,原先第二条岔路是直接进入的,但是这里先判断加入第 index 件物品后能否满足容量不超过 V 的要求,只有当条件满足时才更新最大价值以及进入这条岔路,这样可以降低计算量,使算法在数据不极端时有很好的表现。
这种通过题目条件的限制来节省 DFS 计算量的方法称作剪枝(前提是剪枝后算法仍然正确)。
剪枝是一门艺术,学会灵活运用题目中给出的条件,可以使得代码的计算量大大降低,很多题目甚至可以使时间复杂度下降好几个等级。
事实上,上面的这个问题给出了一类常见 DFS 问题的解决方法,即给定一个序列,枚举这个序列的所有子序列(可以不连续)。
例如对序列{1,2,3}来说,它的所有子序列为{1}、{2}、{3}、{1,2}、{1,3}、{2,3}、{1,2,3}。
枚举所有子序列的目的很明显—可以从中选择一个"最优"子序列,使它的某个特征是所有子序列中最优的;如果有需要,还可以把这个最优子序列保存下来。
显然,这个问题也等价于枚举从 N 个整数中选择 K 个数的所有方案。
例如这样一个问题:给定 N 个整数(可能有负数),从中选择 K 个数,使得这 K 个数之和恰好等于一个给定的整数 X;
如果有多种方案,选择它们中元素平方和最大的一个。数据保证这样的方案唯一。例如,从4个整数{2,3.3.4}中选择2个数,使它们的和为6,显然有两种方案 {2,4} 与 {3,3} ,其中平方和最大的方案为 {2,4} 。
与之前的问题类似,此处仍然需要记录当前处理的整数编号 index;由于要求恰好选择 K 个数,因此需要一个参数 nowK 来记录当前已经选择的数的个数;另外,还需要参数 sum 和 sumSqu 分别记录当前已选整数之和与平方和。
于是 DFS 就是下面这个样子:
void DFS(int index,int nowK,int sum,int sumSqu){...}
此处主要讲解如何保存最优方案,即平方和最大的方案。
首先,需要一个数组 temp,用以存放当前已经选择的整数。
这样,当试图进入"选 index 号数" 这条分支时,就把 A[index] 加入 temp 中;
而当这条分支结束时,就把它从 temp 中去除,使它不会影响 “不选 index 号数” 这条分支。
接着,如果在某个时候发现当前已经选择了 K 个数,且这 K 个数之和恰好为 x 时,就去判断平方和是否比已有的最大平方和 maxSumSqu 还要大:
如果确实更大,那么说明找到了更优的方案,把 temp 赋给用以存放最优方案的数组 ans。
这样,当所有方案都枚举完毕后,ans 存放的就是最优方案,maxSumSqu 存放的就是对应的最优值。
下面给出了主要部分的代码,建议大家能完整理解并自行写出:
//序列 A 中 n 个数选 k 个数使得和为 x ,最大平方和为 maxSumSqu int n,k,x,maxSumSqu=-1,A[maxn];
//temp 存放临时方案,ans 存放平方和最大的方案 vector<int> temp,ans;
//当前处理 index 号整数,当前已选整数个数为 nowK //当前已选整数之和为 sum,当前已选整数平方和为sumSqu void DFS(int index,int nowK,int sum,int sumSqu)
{
if(nowK==k&&sum==x)
{
//找到k个数的和为x //如果比当前找到的更优 if(sumSqu>maxSumSqu)
{
//更新最大平方和 maxSumSqu=sumSqu;
ans=temp; //更新最优方案 }
return;
}
//已经处理完 n 个数,或者超过 k 个数,或者和超过 x ,返回 if(index==n||nowK>k||sum>x) return;
//选index号数 temp.push_back(A[index]);
DFS(index+1,nowK+1,sum+A[index],sumSqu+A[index]*A[index]);
temp.pop_back();
//不选 index号数 DFS(index+1,nowK,sum,sumSqu);
}
上面这个问题中的每个数都只能选择一次,现在稍微修改题目;假设 N 个整数中的每一个都可以被选择多次,那么选择 K 个数,使得 K 个数之和恰好为 X 。
例如有三个整数 1、4、7,需要从中选择 5 个数,使得这 5 个数之和为 17 。
显然,只需要选择 3 个 1 和2个7,即可得到17。
这个问题只需要对上面的代码进行少量的修改即可。由于每个整数都可以被选择多次,因此当选择了 index 号数时,不应当直接进入 index +1 号数的处理。
显然,应当能够继续选择 index 号数,直到某个时刻决定不再选择 index 号数,就会通过"不选 index 号数"这条分支进入 index+1 号数的处理。
因此只需要把" 选 index号数"这条分支的代码修改为DFS(index,nowK+1, sum+A[index], sumSqu+A[index]*A[index]) 即可。