如要转载,请注明原创出处:https://zhuanlan.zhihu.com/p/105917577
我记得大一的时候,《计算机基础》第一章内容就会讲到计算机编码。期末考试的时候,老师会有这样的考题:求出一个数的补码。我能清楚的记得步骤是:先判断数的正负。正数的补码是其原码本身;而负数的补码是先求反码,然后再让反码加1。
所以,计算机会有3种码:原码、反码和补码。你翻开所有的计算机教科书,几乎都会讲到这块内容,但是却没有一本教程会告诉你:为什么计算机需要这三种码?
如果你是爱思考的,特别是计算机系的学生,在学习的过程中就应该自己会主动思考这个问题。在我自学计算机的过程中,显然这个问题也困扰到了我,当时还不会网络搜索,但是我自己在整理学习笔记的过程中,找到了下面两张已经泛黄的草稿纸:
这个就是当时自己独立思考的过程。今天来看,总体结论是对的,但是阅读起来不是很顺畅和清晰。所以今天我就重新整理一下思路和逻辑,正式对“计算机为什么要用反码和补码?”这个问题做出推论解释。
一、为什么需要反码?
反码的作用就相当于数学中的负数。
对于小学生来说,会做的算术题是:5-3,但是不会做3-5。于是,我们上初中的时候,数学里就引进了一个新的概念:负数。引入负数之后,本来是减法的运算就可以变成加法来实现:
3-5=3+[-5]=[-2],中括号代表“负数”,“负数”就是我们人为给出的数学术语。
对于计算机来说,会做的算术题是:5+3,但是不会做3-5。于是,我们就在编码里引进了一个新的概念:反码。引入反码之后,本来是减法的运算就可以变成加法来实现:
3-5=3+[-5]=[-2],中括号代表“反码”,“反码”就是我们人为给出的计算机术语。
这里,你一定有一个疑问:为什么计算机只会做5+3,不会做3-5。这是因为在计算机的数字电路中只有加法器,没有所谓的“减法器”。不是说计算机厂商不会设计减法器,因为聪明的人既然发明了方法能够用加法来实现减法操作,那为什么还需要画蛇添足的弄一个减法器?
接着说:那么反码要怎么定义才能实现减法变加法的功能呢?聪明的人想的办法如下:
1.正数的反码保持原码不变:3=[0_0000011]
2.负数除最高位(正负符号位)外,全部取反(0变1,1变0):-5=1_0000101取反=[1_1111010]
于是3+[-5]=[-2]的计算过程为:
[0_0000011]+[1_1111010]=[1_11111101]
这样,这种反码方法就成功实现了目标!至于为什么,我想只有数学家能给出解释了。
二、为什么需要补码?
都是因为“0”这个特殊数字的存在。
先问你一个问题:0是正数还是负数?你肯定会说:0既不是正数也不是负数,这是我们初中学到的数学知识。这个回答没有问题,所以以后每次碰到0,人们都不会把它当正数或负数。
那么计算机呢?计算机不同于人脑,计算机在碰到任何数字之前只根据最高位的符号位来判断正负性,“0”表示正数,“1”表示负数。
前面我们推论了为何要用反码,那么用8位二进制反码表示的正数范围: +0 —— +127;负数范围: -127 —— -0。但是,其中有两个特殊的编码会出现:
[0_0000000]=+0 (反码)
[1_1111111]=-0 (反码)
其实,+0和-0代表的都是0。这样一来,“0”这个数字在计算机中的编码就不是唯一的了。对于计算机来说,这是绝对不行的,因为任何数字都只能有1个编码。
于是,聪明的人就做了这样一个决定:把0当成正数,也即+0,这样0的编码就变成:0_0000000。那8位二进制表示的正数范围仍然是: +0 —— +127。
但是,对于负数就必须要做调整,也即-0必须要让位—1_1111111这个编码不能表示-0。我们可以把负数整体向后“挪动1位”:只要将8位二进制表示的负数范围从:-127 —— -0变成:-128 —— -1,就能成功解决问题。
那么怎么整体挪动1位呢?方法就是反码+1。{1_1111111}编码就不再表示-0,而变成了-1。顺着推,最小的编码{1_0000000}就是-128。
我们给这个反码+1又人为的取了一个新的名字,叫补码。于是乎,补码的定义如下:
1.正数的补码保持原码不变:3={0_0000011}
2.负数先求反码,然后再加1:-5=[1_1111010]+1={1_1111011}
于是3+{-5}={-2}的计算过程为:
{0_0000011}+{1_1111011}={11111110}
至此,通过补码就成功解决了数字0在计算机中非唯一编码的问题,且也能实现减法变加法。
所以,在计算机的世界里,0是正数。这点和我们学的数学不一样。
{0_1111111}=+127 (补码)
{0_0000000}=+0 (补码)
{1_1111111}=-1 (补码)
{1_0000000}=-128 (补码)
三、真机演示
说了这么多,计算机内部电路是不是按我们上面的理论来的呢?我们必须要真机演示体会一下:
预设: AX=3,BX=5,CX=-5。DX用于存放运算结果。
- 正数加法:AX+BX
MOV AL,3
MOV BL,5
ADD AL,BL
MOV DL,AL
将汇编程序保存为code.asm,用NASM编译成EXE:
![]()
![]()
然后用Turbo-Debugger调试器调试:


按F8可以逐步调试:


AX=3

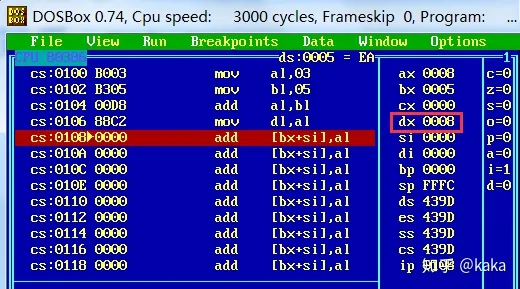
可以看到AX,BX和DX都是原码,也即正数的补码就是原码。
- 正数减法:AX-BX
MOV AL,3
MOV BL,5
SUB AL,BL
MOV DL,AL


可以看到,这次减法之后,结果是0XFE={11111110}={-2},成功验证之前的推论:
于是3-5={3}+{-5}={-2}的计算过程为:
{0_0000011}补码+{1_1111011}补码={11111110} 补码
我前面说过,减法的运算过程是把减法变加法:3-5={3}+{-5},所以这里肯定是要先把减数BX的值5转换成-5的补码,但是我们看到程序运行过程中BX的值一直都是05,并没有变成-5的补码,这是怎么回事?因为减法变加法只是CPU的一个运算过程,它并不会去修改参与运算数存储的值,你可以理解为CPU从BX里面把5取出来之后,有专门的电路负责把它变成-5的补码,或者有专门另外隐藏的寄存器用来存放它的补码,然后再参与加法运算。BX的值是我们人为赋予的5,当然不能为了做这样一个减法而随意去修改它。
3. 正负数加法:AX+CX
MOV AL,3
MOV CL,-5
ADD AL,CL
MOV DL,AL
下图表明,计算机看到CX是负数,直接就编码成补码进行存储了:0XFB={11111011}={-5}。那么计算机是怎么把CX=-5存储为补码0XFB的呢?是不是要严格按我们之前介绍的步骤呢:
(a) 正数原码=00001001
(b) 负数原码=10001001
(b) 反码=11110110 (除符号位取反)
(c) 补码:=反码+1=11110111=0XFB
这个问题,在下一小节会有明确答案。

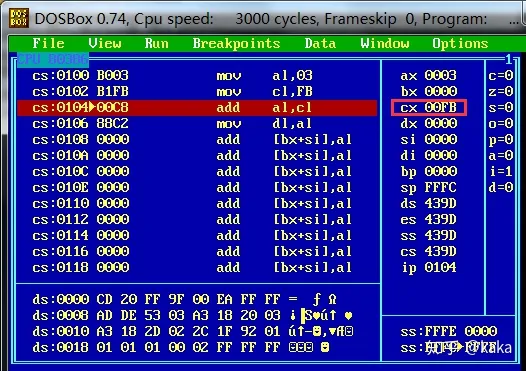
负数CX直接存储为补码
运算之后的结果如下图:结果是0XFE={11111110}={-2},这个运算过程是:
{3}+{-5}={-2}


4.正负数减法:AX-CX

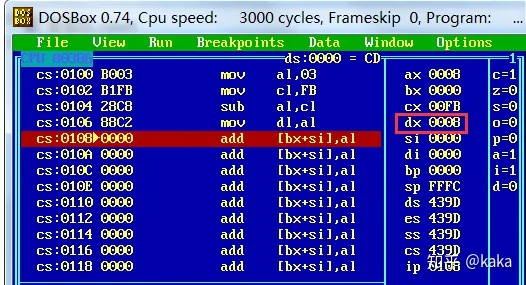
运算结果:0X08={00001000}={8},也即:3-(-5)=3+(-(-5))=3+5=8。
那么问题来了,(-(-5))这个计算机怎么操作?你肯定会说“负负得正”,但计算机哪里会懂。由于所有的减法变加法,其实都是一样的规则—取减数相反数相加:
A-B=A+(-B)。
那么我只要设计出一种方法能够计算任何数的相反数就行了,而计算机计算相反数的方法是:
相反数=反码+1 :-B=~B+1,这里的B可以是任何数,不用区分正负和考虑符号位!
所以,(-(-5))的过程就是计算机需要2次取相反数进行编码:
(a) 第1次对-5进行编码—规则:[5的反码]+1=00000101取反+1=11111011
(b) 第2次对-(-5)进行编码—规则[-5的反码]+1=11111011取反+1=00000101,实际上又回到了5的编码,相当于“负负得正”。
虽然都是反码+1,但是这个和我们前面介绍的求负数的补码方法有差异:那里求负数反码的时候,是符号位除外了的。而这里求相反数是所有位都全部取反。
计算机里面有了相反数的概念,就能统一所有的运算法则:负数就是求正数的相反数,减法就是求减数的相反数再相加。所以,我们可以把上一节中CX=-5的存储过程做进一步的优化:
(a) 5的原码=00001001
(b) 全部取反=11110110
(c) 补码:=反码+1=11110111=0XFB
我觉得这个才是计算机真正的编码过程,因为它在编码的时候不需要考虑和判断所谓的第一位正负号“符号位”,只要看到符号“-”就重复“反码+1”的取相反数过程。
4.负数减法
根据上述过程,那么可以推论最复杂的负数减法过程:如AX=-3,BX=-2,我们要计算这两个负数相减:DX=AX-BX,过程应该是:
(a) AX存入被减数:由于计算机见到有负号"-",那么需对3做一次取相反数的操作:原码3取反后+1:00000011取反+1=11111101=0XFD。
(b) BX存入减数: 由于计算机见到有负号"-",那么需对2做一次取相反数的操作:原码2取反后+1:00000010取反+1=11111110=0XFE。
(c) DX=AX-BX:计算机先把减法变加法,AX-BX=AX+(-BX),由于计算机见到第二个加数有负号"-",那需对BX做一次取相反数的操作:BX取反+1=11111110取反+1=00000010。
(d) 计算加法:AX+(-BX)=11111101+00000010=11111111=0XFF={-1}
该过程的计算机验证截图如下:


所以,从上面的过程可以清楚的看到计算机最重要的就是:“反码+1”,反码+1就叫补码。有了补码,计算机才能实现负号“-”的操作,而这个操作是其实就是取相反数的含义。
正是有了取相反数的概念,因此在汇编程序中有这样一条指令:NEG。这个指令就是取相反数,也等同于对数做一个求补(反码+1)的操作。
补码这个取相反数的机制,给计算机带来的好处太多了。它除了使计算机不用区分加减法以外,在加、减运算的时候,硬件层面上还可以不用区分正负数(符号位没有特殊处理)。如对于某一个编码:0xF0,当它存储在内存中的时候,如果是无符号数,应等于240;如果是有符号数,应等于-16。那它究竟是代表哪个数呢?计算机在硬件层面并不需要知道它代表的是240还是-16,因为它是正是负都不影响和别的任何数字做加减操作。比如在与数字2的编码值0x02相加之后,编码值是0xF2,那这个编码值就可以代表是242或-14。
那这个0xF0最终究竟代表的是哪个数字呢?这是编程者需要处理的事情,比如你在C语言中应当把它定义成signed与否。下面,我们必须要举例来说明这个过程:
假如你是把等于-16的变量定义成signed char类型的,当我们的程序中需要应用这个变量的时候,比如printf(%d),C语言标准库里的printf函数首先会从内存里取出变量的值:0xF0,由于变量是有符号类型,它首先根据0xF0符号位是1来判断是一个负数,第一步就将生成一个"-“号放在一个临时字符串的首位。剩下的事情就是将0xF0这个编码转化成10进制对应的数字字符串"16”,关键问题是printf怎么来实现这个转换呢?
通过前面的推论,得知:**负数是正数的补码,正数是负数的补码,它们互为相反数。**现在,我们要求正数的编码,当然只需要在负数补码的基础上去一次相反数即可,因此对0xF0取相反数就会是如下过程:
0xF0取相反数=1111_0000取相反数=11110000反码+1=00001111+1=0001_0000=16D
虽然得到了16这个数值,但是它和字符串"16"是两回事,printf最终是要把"-"号和"16"相连接组成这个变量完整的字符串才行。那数字16又怎么转化成字符串"16"呢?
方法是我们要在10进制数据中需要逐位获取:先取出最高位数字1,然后把1转化成字符“1”;再取最低位数字6,把6转化成字符“6”。由于每个数字x与它们对应字符的ASCII码值关系是:ASCII码=48+ x。因此,我们将取得的数字加上1+48=49,6+48=54,那么就得到了两个字符"1"和"6"。printf把字符"1"和"6"依次连接在字符"-“后面,就得到了最终完整的字符串:”-16"。最后printf再调用操作系统字符串显示API,才能完整的在屏幕上显示出"-16"!
通过这个案例,我们可以看出高级语言对计算机底层编码的处理过程,相对来说不简单,因此高级语言会屏蔽掉计算机底层很多的细节。
接着上面这个0xF0,我们再扯远点。甚至于硬件层面都不知道0xF0代表的是一个数字(数据)呢,还是一条机器指令。那也是编程者需要关心和设计的事情:当程序在内存里运行到这个0xF0存储位置的时候,它代表的就应该是一条机器指令;而当程序需要从内存里取出这个0xF0值的时候,它代表的就应该是一个数字(数据)。
继续扯回来。虽然计算机硬件层面上加、减运算的时候,可以不用区分正数、负数,但是在乘除法的时候就不行了。比如现在有一个被除数编码:0x01E0,一个除数编码:0xF0。0x01E0代表的是数480。0xF0可能代表240,也可能代表-16。计算结果480/240=2或480/-16=-30。2的编码是0x02,而-30的编码是0xE2,显然这两个编码不能统一(因为符号位参与了计算过程),因此你在做乘除法之前,就必须在硬件层面指定0xF0代表的是正数240还是负数-16。正因为如此,汇编程序在做乘除法的时候,必须要指定是无符号乘除还是有符号乘除,无符号除法用指令:DIV,有符号除法用指令:IDIV。
四、总结
最终,计算机数字的3种编码—原码、反码和补码,我们用一句话来总结如下:
原码:是对自然正数(包括0)的二进制编码,正数在计算机中直接用原码进行存储。
**反码:**可以理解为是求补码的中间过程,反码=原码逐位取反。计算机并不存储反码。
补码:计算机求相反数的编码,补码=反码+1。负数在计算机中使用补码进行存储。
但是,归根到底,我们可以说计算机是用补码进行存储的。为什么?因为原码=对应相反数的补码,实际上也是补码,只不过是负数的补码。



